Solving Two-Step Equations: A Comprehensive Guide with PDF Resources
Master two-step equations with this comprehensive guide. It offers fundamental concepts, a clear step-by-step methodology, and access to free PDF worksheets. These valuable resources, complete with answer keys and diverse problems, ensure effective practice for algebra success.
After mastering one-step equations, we advance to two-step equations. These foundational algebraic expressions require two distinct operations to isolate the variable. Understanding their structure is crucial for progressing in algebra, setting the stage for more complex problem-solving scenarios efficiently.
Defining Two-Step Equations

A two-step equation is a fundamental algebraic expression that requires precisely two distinct mathematical operations to be performed to isolate the unknown variable. These equations build directly upon the foundational understanding of one-step equations, introducing a slightly increased level of complexity for students. Typically, a two-step equation involves both an addition or subtraction component and a multiplication or division component, all acting upon the variable. For instance, an equation such as “3y ─ 6 = 12” or “x/4 + 5 = 9” exemplifies this structure, where a variable is combined with constants through two different operations. The designation “two-step” directly refers to the minimum number of inverse operations necessary to determine the variable’s value. Understanding this definition is the crucial initial step before one can successfully apply the systematic methodology for solving them. It helps solidify how terms interact within an equation and clarifies the ultimate objective: finding the specific numerical solution for the unknown.
Objective: Isolating the Variable
The primary and most crucial objective when approaching any algebraic equation, especially two-step equations, is the successful isolation of the variable. This fundamental goal means systematically manipulating the equation until the unknown variable, such as ‘x’ or ‘y’, stands completely alone on one side of the equals sign, with a definitive numerical value on the opposing side. Achieving this isolation effectively reveals the unique solution to the equation, providing the specific number that satisfies and makes the original mathematical statement true. For example, transforming an equation like 2x ─ 8 = 16 into the form x = (a single numerical value) exemplifies this aim. This process of isolating the variable is absolutely central to all algebraic problem-solving, enabling us to precisely determine unknown quantities within various mathematical and real-world contexts. It inherently demands a clear understanding that any operation performed to remove terms from the variable’s side must be applied with perfect consistency to both sides of the equation to rigorously maintain its essential balance. The ultimate aim is to progressively simplify the equation, systematically stripping away all associated coefficients and constant terms until the variable is entirely by itself, thereby unequivocally obtaining its true value. Without successfully isolating the variable, the equation remains fundamentally unsolved, and its underlying numerical relationship remains obscured, rendering the problem incomplete. This singular objective underpins all effective strategies for solving two-step equations efficiently.

Fundamental Concepts for Solving Two-Step Equations
Solving two-step equations relies on key principles: understanding inverse (opposite) operations to undo steps, maintaining equation balance by applying operations equally to both sides, and collecting like terms before isolating the variable. These fundamental concepts are crucial.
Understanding Inverse Operations
A foundational element for solving two-step equations is understanding inverse operations. These are “opposite” mathematical actions designed to cancel each other, crucial for isolating the variable efficiently. Every arithmetic operation possesses a unique inverse: addition undoes subtraction, and subtraction reverses addition. Similarly, multiplication is the inverse of division, and division acts as the inverse of multiplication. The main objective in solving any equation is to systematically remove all numbers or operations attached to the variable. This is achieved by applying the appropriate inverse operation. For instance, if a number is added, you subtract it from both sides. If the variable is multiplied, you divide both sides by that number. This strategic application of inverse operations enables the logical dismantling of an equation, simplifying it step-by-step. It transforms complex problems into direct statements of the variable’s value, making algebraic solutions accessible. Mastery of these opposite operations is truly indispensable for proficiency.
The Principle of Balancing Equations
The core principle of balancing equations is fundamental to solving two-step equations and indeed, all algebraic equations. It dictates that whatever operation you perform on one side of an equation, you must perform the exact same operation on the other side. This ensures that the equality of the equation remains intact, much like keeping a balance scale level. If you add a value to one side, you must add the same value to the other. If you subtract, multiply, or divide by a number on one side, the identical action must be applied to the other side. This principle is explicitly mentioned as a big idea for solving two-step equations, emphasizing its critical role. It allows for the systematic isolation of the variable without altering the equation’s true solution. By consistently applying this balancing act, combined with inverse operations, we can simplify complex expressions into solvable forms, leading directly to the variable’s value.
Collecting Like Terms Before Isolating
In the process of solving two-step equations, a crucial preliminary step, especially when variables or constants appear multiple times or are scattered across one or both sides, is to collect all like terms. This “BIG IDEA” explicitly emphasizes simplifying the equation’s appearance before systematically isolating the variable. Like terms are precisely defined as those algebraic components that possess the exact same variable raised to the same power, or are simply numerical constants. By effectively combining these similar terms, you significantly reduce the overall number of distinct individual components within the equation, consequently making it substantially cleaner, more organized, and easier to manage. For instance, if an equation contains an expression such as 3x + 5 + 2x on one side, collecting like terms efficiently transforms it into the much simpler form of 5x + 5. This essential simplification must be meticulously completed on each side of the equation independently first. Once all similar terms are thoroughly combined, the equation then presents a remarkably clearer and more direct path forward for applying the necessary inverse operations and strictly adhering to the fundamental principle of balancing equations. This systematic preparatory approach proactively prevents common algebraic errors, streamlines the entire solution process, and ultimately leads to more efficient and accurate variable isolation. It is fundamentally about decluttering the algebraic expression to reveal its core two-step structure for precise solving.

Step-by-Step Methodology for Solving Two-Step Equations
This section outlines the systematic approach to solving two-step equations. It details the precise order of operations—undoing addition/subtraction, then multiplication/division—and emphasizes simplifying both sides for clarity and accuracy.
Step 1: Undoing Addition or Subtraction
The initial crucial step in solving any two-step equation involves isolating the term containing the variable by eliminating any constant terms that are added to or subtracted from it. This is achieved by applying the inverse operation to both sides of the equation, a fundamental principle for maintaining equality. If a constant is being added to the variable term, you must subtract that exact constant from both sides of the equation. Conversely, if a constant is being subtracted from the variable term, you will add that constant to both sides. This action effectively cancels out the constant on the side with the variable, moving it to the other side of the equal sign. For instance, in an equation like 2x + 5 = 21, the first move is to subtract 5 from both the left and right sides to undo the addition. Similarly, for 3y ─ 6 = 12, you would add 6 to both sides. This methodical application of inverse operations ensures the equation remains balanced, progressively simplifying it towards isolating the unknown variable. Remember, whatever operation you perform on one side, you must replicate precisely on the other side to preserve the equation’s truth. This preliminary step prepares the equation for the subsequent operation, making it easier to solve.
Step 2: Undoing Multiplication or Division
After successfully completing the first step of undoing addition or subtraction, you will typically be left with an equation where the variable is either multiplied or divided by a constant. This brings us to the second crucial phase: undoing multiplication or division to finally isolate the variable. The principle of inverse operations remains paramount here. If your equation now looks like ax = b (where ‘a’ is a coefficient multiplying the variable ‘x’), you must divide both sides of the equation by ‘a’. This action cancels out the coefficient on the variable’s side, leaving ‘x’ by itself. For instance, if you have 2x = 16, you would divide both sides by 2 to find x = 8. Conversely, if the variable is being divided by a number, such as in x/a = b, the inverse operation is multiplication. You would multiply both sides of the equation by ‘a’ to cancel out the denominator and solve for ‘x’. An example would be k/2 = 6, where multiplying both sides by 2 yields k = 12. It is vital to consistently apply the chosen inverse operation to both sides of the equation to preserve its equality and arrive at the correct solution for the variable. This systematic approach completes the process of solving two-step equations.
Simplifying Both Sides of the Equation
Before embarking on the process of isolating the variable through inverse operations, an essential preliminary step in solving two-step equations is to simplify both sides of the equation. This crucial action involves combining any like terms present on either the left or right side of the equal sign. For instance, if an equation contains multiple constant terms or several terms with the same variable on one side, these should be consolidated into single terms. This simplification makes the equation much more manageable and less prone to errors in subsequent steps. As a core “big idea” in solving equations, collecting like terms on each side streamlines the expression, reducing it to its most concise form. This might involve performing basic arithmetic such as addition, subtraction, or even distribution if parentheses are involved. By simplifying thoroughly at the outset, you effectively reduce the complexity of the equation, setting a clear foundation before applying the properties of equality to move terms across the equal sign. This ensures that when you begin to undo addition, subtraction, multiplication, or division, you are working with the most straightforward representation of the problem.
Practice and Resources: Two-Step Equations PDF Worksheets
Access a free library of two-step equations PDF worksheets, perfect for practice. Each worksheet comes with a complete answer key, offering problems with integers, decimals, and fractions. These resources are ideal for 6th, 7th, and 8th-grade students to master solving equations.
Accessing Free Two-Step Equations Worksheets PDF

Embark on your journey to master two-step equations by easily accessing a wealth of free PDF worksheets. These invaluable resources are readily available for download, providing a robust platform for extra practice. The comprehensive worksheet library encompasses numerous PDF files, each meticulously designed to reinforce your understanding of linear equations. Students seeking to hone their algebraic skills will find these printable pages exceptionally beneficial. Whether you are in 6th, 7th, or 8th grade, these beginning algebra worksheets cater to various skill levels and learning needs, offering a wide array of problems. Some platforms also provide dedicated PDF guides that include clear step-by-step solutions, additional practice problems, and expert tips, making your learning process both effortless and highly effective. Downloading these free practice pages allows you to solve and verify two-step equations at your own pace, securing a strong foundation in algebra. Many resources offer these files for free, ensuring widespread accessibility for all learners, thereby enhancing educational opportunities.
Complete Answer Keys for Practice PDFs
To maximize the effectiveness of your practice, every downloadable two-step equations worksheet comes equipped with a comprehensive answer key. These complete answer keys are an integral part of the learning process, providing immediate feedback on your solutions. Typically, you will find the full answer keys conveniently located on the second page of each PDF file, making it easy to check your work after attempting the problems. This allows students to not only solve equations but also to verify their understanding and identify any areas needing further review. Having a complete set of solutions empowers learners to self-assess accurately, reinforcing correct methods and helping to correct misconceptions promptly. Whether you are working on problems involving integers, decimals, or fractions, the detailed answer keys ensure that you can confidently check every single step and the final answer. They serve as an invaluable tool for both independent study and guided practice, ensuring that you grasp the principles of balancing equations and inverse operations, ultimately securing your path to algebra success.
Variety of Problems: Integers, Decimals, Fractions
The practice worksheets for solving two-step equations offer a rich diversity of problem types, ensuring a truly comprehensive learning experience. To fully master these algebraic concepts, students need exposure to equations that extend beyond simple whole numbers. Therefore, our resources include problems featuring integers, which solidify foundational understanding of positive and negative numbers. Furthermore, the collection extends to equations incorporating decimals, challenging learners to apply arithmetic skills in a slightly different context while maintaining core principles of inverse operations and balancing. Crucially, a significant portion of the worksheets is dedicated to equations involving fractions, often perceived as more complex. This variety ensures students develop flexibility in their problem-solving approaches, preparing them for more advanced mathematics. By tackling equations with integers, decimals, and fractions, students gain a robust understanding of how to manipulate different number forms within a two-step equation framework. This broad spectrum of problems is designed to cater to various math operations, strengthening algebraic proficiency across the board. The ultimate goal is to build confidence and competence in handling any two-step equation, irrespective of its numerical format.
Worksheets for 6th, 7th, and 8th Grade Students
Our comprehensive library of two-step equations PDF worksheets is specifically designed to cater to the developmental stages of students across various middle school grades. These beginning algebra worksheets provide appropriate and targeted practice for 6th grade students, introducing them to foundational algebraic concepts in an accessible manner. For 7th grade students, the materials offer a crucial bridge, solidifying their understanding of equation solving and preparing them for more complex algebraic tasks. Moving into 8th grade, the worksheets continue to be highly relevant, allowing students to refine their skills and tackle more challenging problems involving integers, decimals, and fractions, as they prepare for high school algebra. Each worksheet is crafted to support the curriculum standards for these grade levels, ensuring that the content is both relevant and effective for student learning. The inclusion of full answer keys on the second page of each PDF file makes these resources ideal for both classroom instruction and independent practice at home. This structured approach ensures that students, regardless of their current grade level within this range, can find suitable materials to enhance their proficiency in solving two-step equations.
Solving Two-Step Equations with Variables on Both Sides

Expanding on the foundational skills of solving basic two-step equations, students will encounter more complex scenarios where variables appear on both sides of the equal sign. This introduces an additional layer to the problem-solving process, requiring careful application of inverse operations to consolidate terms. The primary objective remains isolating the variable, but now it involves an initial step of gathering all variable terms onto one side of the equation and all constant terms onto the other. This often means utilizing the addition or subtraction properties of equality multiple times before proceeding to undo multiplication or division. It is crucial to simplify each side of the equation first, if necessary, by combining like terms before attempting to move terms across the equal sign. This systematic approach ensures clarity and accuracy in reaching the solution. To master this advanced type of equation, dedicated practice is essential. Resources, such as specialized worksheets, are available to provide ample opportunities for students to solve two-step equations where variables are present on both sides. These practice problems, often including complete solutions, help reinforce the methodology and build confidence in tackling more intricate algebraic challenges, preparing learners for higher-level mathematics.
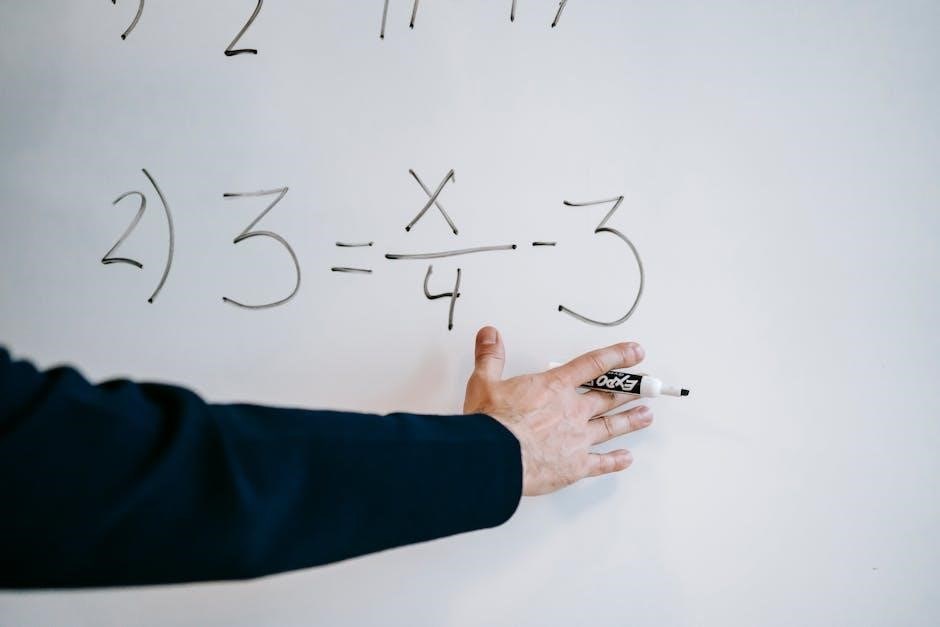
Verifying Your Solution: Checking Answers
After successfully solving a two-step equation and determining a value for the variable, verifying your solution is a crucial final step. This process ensures accuracy and reinforces your understanding of the algebraic principles involved. To check your answer, you must substitute the numerical value obtained for the variable back into the original equation. For example, if your solution for ‘x’ was 5, you would replace all instances of ‘x’ in the initial problem with ‘5’.
Following this substitution, carefully evaluate both sides of the equation independently, adhering strictly to the order of operations. If your calculated solution is correct, the numerical result on the left side of the equation will precisely match the numerical result on the right side. This equality confirms the validity of your answer. Should the two sides not balance, it signals an error in your solving process, necessitating a review of your steps to pinpoint the mistake. This self-correction phase is invaluable for learning. Practice resources, like the provided PDF worksheets with answer keys, greatly facilitate this verification, allowing students to efficiently confirm their work and deepen their mastery of two-step equations.